Сценарий мастер класса учителя математики

Чернышова Надежда Станиславовна,

учитель математики Караульского филиала им. Б.Н. Чичерина МБОУ «Инжавинская СОШ»

Мастер – класс  «Удивительное  рядом»

Незнающие пусть научатся,

            а знающие — вспомнят еще раз.

                        Античный афоризм

Цели:

• изучение  быстрого  счёта с использованием нестандартных приёмов

 устного счёта, познакомить с упрощёнными  приёмами устных

 вычислений, когда вычисляющий не имеет в своём распоряжении

таблиц и калькулятора

Задачи:

• рассмотреть и показать на примерах применение нестандартных

способов умножения чисел;

• сформировать прочные вычислительные навыки,

 развивать интеллектуальные способности, расширять математический кругозор, формировать  устойчивый  интерес к математике.

Оборудование: проектор, экран, компьютер, бумага, карандаш.

Слайд 1.

Здравствуйте уважаемые коллеги! Поднимите руки, кто в этом зале любит МАТЕМАТИКУ. Поднимите руки, кто в этом зале не любит МАТЕМАТИКУ. Что удивительного вы заметили? Очень приятно, что сегодня собрались те, кто математику….

Я долго думала, что же мне показать на мастер-классе? Чему я могу научить и удивить взрослых, состоявшихся людей?

Слайд 2.

Сначала я хотела показать решение уравнений n-х степеней с помощью схемы Горнера. В школе согласно государственных стандартов мы не решаем уравнения используя данную схему – но решила, что это очень сложно…

Слайд 3.

          Затем я хотела показать вам нахождение площадей геометрических фигур. Данная тема – обязательное задание в ЕГЭ, а теперь и в ОГЭ. Для математиков она очень актуальна: фигур множество, соответственно формул площадей – тоже – а дети их если сразу не выучили, то потом, обязательно забудут.

Слайд 4.

Мне хотелось показать одну единственную, универсальную формулу (формулу Пика) с помощью которой даже слабый ученик всегда может посчитать площадь фигур – одну формулу он всегда запомнит. Но, потом подумала – а зачем – это вам надо?

 «Великая книга природы написана математическими символами».(Галилей).  Математика очень многогранная наука и охватить все в ней просто не возможно.

Слайд 5

Давным-давно один восточный владыка, просвещенный и мудрый, пожелал узнать все о математике всех времен и народов. Вызвал он приближенных и объявил им свою волю.

— Повелеваю,- молвил он,- написать мне все о математике. Как она возникла, какой была раньше, какой стала теперь, какой будет в будущем. Собрать мне все математические знания, что есть в мире, А самое главное ответьте на вопрос  – что это… математика.

И дал на это пять лет сроку.

         Со всего царства были собраны мудрейшие из мудрецов, и им объявили желание владыки.

Миновало пять лет, и явились приближенные во дворец.

— О, великий господин, срок названный тобой ничтожно мал. Мы не успели собрать даже тысячной доли тех знаний, о которых ты говорил, и мы не успели дать ответ на твой главный вопрос.

Рассердился владыка, но выглянув в окно увидел, что перед дворцом выстроился караван верблюдов такой длинный, что конец его терялся где-то за горизонтом. И на каждом верблюде нагружено по два громадных тюка. А в каждом тюке было по десять толстенных томов.

— Вы смеетесь надо мной! — рассердился владыка. — Да ведь я до конца своей жизни не успею прочесть и десятой доли того, что они собрали! Нет, пусть напишут мне краткую историю математики.

— Пусть напишут мне самое-самое главное. Сколько времени нужно на это?

— Завтра, о владыка. Ты получишь то, что желаешь!

— Завтра? — удивился правитель.- Хорошо.

… Едва солнце взошло на лазурном небе, как владыка потребовал к себе мудреца. Мудрец вошел, неся в руках маленький ларец из сандалового дерева;

— Ты найдешь в нем, о владыка, самое главное в математике всех времен и народов, — произнес мудрец.

Но прежде, чем откроем ларец и прочитаем, что там написано, я предлагаю вам несколько задач, которые могут вызвать удивление. Кто знает, может быть, и они были записаны мудрецами в тех толстенных томах

И согласитесь, что охватить все математические знания невозможно.

Но мы перед собой такую цель не ставим…

Слайд 6

Давайте окунемся в атмосферу востока.… Закройте глаза, представьте, что вы сидите на уютной террасе, наполняете чашку чаем и ответьте на вопрос: с чем ассоциируется у вас слово «господин», «владыка», «чай», «математика»

Конечно с Китаем.  На востоке, за чашкой чая ведут не только светские беседы, но и переговоры. А китайских школах чай можно пить практически в любое время (даже на уроке). А ведь и чайные пакетики придумали в Китае.

Одна из сложных тем математики – умножение многозначных чисел. Умножать начинают в начальной школе, но и в 5, а порой и в 9 классе всегда найдется ученик для кого данная операция дается с трудом… Да и сильный ученик очень часто, допустив ошибку при вычислениях, при проверке – в 50% случаев допускает ту же ошибку.

Большинство взрослых и детей знают, как умножать числа только столбиком – то есть умножают каждую цифру на каждую, а потом суммируют результаты.

Но ведь есть множество и других методов… И эти способы математики называют «китайскими»:

Китайцы считают математику высшей наукой – ее основы должен знать каждый… там нет разделения на сильных и слабых учеников – есть способные и не очень,… а научить должны всех (как и мы!!!!)

Слайд 7.

1. Умножение «палочками»

           Для умножения чисел без таблиц умножения, достаточно иметь карандаш и бумагу…

Умножим 21х34 =

Посчитайте столбиком.… А теперь посмотрите, новый для вас способ…                

Я предлагаю разделиться на две группы: 1- будет находить произведение традиционным способом  ( умножением в столбик), а 2 группа – будет находить произведение чисел, используя новый метод.

Умножим  42х23=

Ответ совпал. Отлично. Для детей, не знающих таблицу умножения – это большое подспорье в выполнении заданий (А кто сказал, что мы должны учить детей считать только  столбиком? в стандартах об этом ни слова!!!!)

Конечно, этот способ имеет свои недостатки: долго приходится считать узлы решетки, если в состав числа входят числа 7,8,9.

Слайд 8.

2. Умножение в «прямоугольнике».

Здесь таблицу умножения надо знать, но зато этот способ применяется при решении «больших примеров», т.е. умножении многозначных чисел. В каждый квадрат впишем произведение цифр, расположенных в одной строке и одном столбце  с  этим квадратом. Десятки располагаются в верхнем треугольнике, а единицы – в нижнем. Цифры складываются  вдоль каждой диагонали.  Результаты записываются  слева и  справа от таблицы.

654х44 = (28776).  

Проверьте верность моих утверждений, умножив числа 155х22=3410 (при умножении 1х2 = 02!!!)

Слайд 9,10

Способ 3,4  «Умножение числа на 11, 111, …

Следует раздвинуть цифры числа, умножаемого на 11, 111…и в образовавшийся промежуток вписать сумму этих цифр.

62*11=682

Слайд 11

Способ  5   «Возведение в квадрат двузначных чисел, оканчивающих на 5»

К числу стоящему в разряде десятков прибавить единицу, полученный результат умножить на это число и в конце приписать двадцать пять, так как 5*5=25.

Слайд 12

Способ 6 « Произведение двузначных чисел в пределах 20» 

Этим способом легко и просто вычислить умножение двузначных чисел, каждое из которых меньше 20 (при больших числах формула не работает)

У математиков на уроках всегда проблемы с устным счетом. Устно дети плохо считают, конечно, это не все способы, которые используют китайцы при объяснении умножения своим детям. Но и этих в полнее достаточно, чтобы все дети в классе начали умножать правильно.  А смогли бы вы за 3 секунды дать ответ? А китайцы могут.

Разминка( гиперссылка)

Еще много разных задач было у мудрецов в том караване, но что, же самое главное поместили они в ларец?

Слайд 13

         Правитель открыл крышку ларца. На бархатной подушке лежал маленький клочок пергамента. Там была написана всего лишь одна фраза: «Математика — это удивление, а через удивление познается мир».

Сегодня я постаралась показать, что познание начинается с удивления. И может быть кто-то из вас посмотрит на математику совсем по-другому…

Цель: познакомить с педагогическим опытом применения задач открытого типа для развития функциональной грамотности обучающихся.

Задачи:

• рассмотреть отличие задач открытого типа от традиционных закрытых задач;
• познакомить с приемами составления открытых задач;
• показать возможности применения открытых задач на уроках и во внеурочной деятельности;
• содействовать профессиональному общению, сотрудничеству.

Ход занятия

Мастер-класс я хотела бы начать с небольшого эксперимента.

Возьмите лист бумаги, линейку и карандаш. Нарисуйте, пожалуйста, 3 отрезка длиной 1 см, 3 см и 5 см. Давайте, посмотрим, что у вас получилось.

Большинство из вас нарисовали 3 параллельных отрезка, расположенных друг под другом. Почему параллельно и друг под другом? Срабатывает стереотипность мышления.

Взрослеем мы сразу после окончания школы, где систематически нас просили последовательно выполнять определенные алгоритмы. Шаг влево, шаг вправо от утвержденного способа решения (а значит и мышления!) — снижение отметки. В этом и есть одна из причин, по которой мы не можем генерировать оригинальную идею, а значит находить самостоятельно решения и справляться с информацией, поступающей из окружающего мира.

Презентация

А теперь внимательно посмотрите на слайд.

— Что вы видите на слайде? Сколько женщин вы видите?

При первом рассмотрении 90% людей видят привлекательную девушку лет 20-25, остальные 10 % видят старуху за 70 с огромным носом. Тем, кто видит картинку впервые, трудно разглядеть второе изображение.

Это картина неоднозначна. Сегодня я хочу вам предложить познакомиться с открытыми задачами. Итак, сегодня мы с вами будем говорить «Задачи в математике и жизни».

Федеральные государственные образовательные стандарты сегодня ориентируют школу не только на предметные, но и на метапредметные и личностные результаты, в том числе на творческое развитие учеников, их готовность к применению универсальных учебных действий в жизненных ситуациях. Для достижения этих целей педагогам необходимо изменение содержания обучения на основе принципов метапредметности, реализация деятельностного характера образования. Учителю необходимо создавать такие условия, при которых у ученика возникало бы желание действовать, причем самостоятельно. Но подавляющее большинство учащихся боятся самостоятельности, тяготеют не к оригинальной мысли, а к разложенной строго по полочкам информации, ориентированы на решение стандартных задач. А в жизни же приходится сталкивается не с учебной задачей, а с реальными жизненными ситуациями.

Одним из возможных путей преодоления данной проблемы является использование открытых задач на различных этапах урока.

Что в этой задаче необычного?

Открытая задача не имеет четкого однозначного условия, в ней может не хватать каких-то данных или, напротив, она может содержать избыточные данные. Поэтому учащемуся необходимо самостоятельно, осмыслить, дополнить, а иногда и сформулировать условие открытой задачи, а также найти необходимые для ее решения сведения. Кроме того, открытая задача может иметь множество путей решения и много верных ответов.

Давайте рассмотрим такие задачи.

1. Владелец одного небольшого ресторана в Америке оказался на грани банкротства. Главная причина — мало посетителей. Он как-то пожаловался на трудности своему другу, а тот неожиданно предложил оригинальную идею. Хозяин попробовал и, через некоторое время клиентов в заведении было хоть отбавляй. Предложите и вы, как завлечь людей в ресторан? Учтите, что повар в ресторане был хороший, обстановка уютная, а сервис на высоте. (Возможны разные варианты ответов. Какой из ответов неправильный? Правильные все.)

В учебном материале мы привыкли к однозначности правильного ответа, который находится в конце учебника. А жизнь дает нам возможность различные пути представления результатов решения возникающих проблем. Значит в урок нужно включать задачи содержащие несколько верных ответов.

2. Маша и Коля ходят в одну и ту же школу. Маша живет в трех километрах от нее, а Коля в пяти. На каком расстоянии друг от друга живут Маша и Коля? (Ответы. Наиболее распространенная ошибка — однозначный ответ на этот вопрос).

Отбор условий, необходимых и достаточных для решения задачи выполнен авторами учебника или учителем. А жизни условия, в которых должна быть решена проблема, во многом остаются неопределенными. Поэтому в школьный урок нужно включать задания с нечетким условием.

3. Маша в саду собирала ягоды. Она набрала две банки смородины и 5 стаканов малины. Сколько ягод набрала Маша? (недостаточно данных)

Такие задачи на уроках практически не встречаются, так как отбор условий, необходимых и достаточных для решения задачи выполнен авторами учебника или учителем. В жизни условия, в которых должна быть решена проблема, во многом остаются неопределенными.

4. В прямоугольнике стороны равны 8 см и 3 см, а периметр 22 см. Найти площадь прямоугольника. (задача с лишними данными)

5. На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие учащиеся 7-11 классов. Голоса между кандидатами распределились в отношении 3:5. Сколько голосов получил победитель? (недостаточно данных)

В школьной задаче цель поставлена заранее. В жизни часто, встречаясь с проблемами, мы много времени тратим на то, чтобы определить для себя, какую именно цель достичь. Это проявление наивысшей степени свободы и активности человека. Значит и в уроке нужно давать возможность цель поставить ребенку самому.

6. Одна матрешка стоит 50 рублей, а вторая — 40 рубля. Задайте вопрос, чтоб текст превратился в задачу.

Человек должен уметь приспосабливаться к изменяющимся условиям. Необходимость усиления творческой составляющей, раскрепощения мысли очевидна. Этому способствует использование в учебном процессе открытых задач.

Мы часто делаем ошибки из-за психологической инертности. Она «заставляет» искать карманы в новой куртке на том же месте, где они были в старой. Нельзя сказать, что она вредна и от нее надо полностью избавляться. Она помогает человеку выполнять привычные действия, даже не задумываясь: мы можем застегнуть одежду или завязать шнурки не глядя; в темноте мы уверенно проходим из одной комнаты в другую. Но при этом она начинает мешать, когда условия изменяются или когда требуется оценить ситуацию с другой, непривычной точки зрения.

Хочу предложить вам следующие задачи. Обязательное условие — решения надо предлагать сразу, без долгих раздумий.

1. На двух руках 10 пальцев? А сколько на десяти руках? (Большинство дают ответ — 100, правильный — 50).
2. Всем хорошо известно, что в поездах стоп-кран ярко-красного цвета. А какого цвета в самолете? Ярко-голубого как небо? Синего? Зеленого? Оранжевого? (В самолете стоп-крана нет).

Иногда нужно «не доверять» самым первым решениям и ответам.

Давайте попробуем побороться с психологической инертностью. Для этого разобьемся на 3 группы. Первая группа отвечает на один и тот же вопрос «Да», вторая «Нет», а третья аргументирует почему «Нет».

Вопросы:

1. Ночью всегда темно?
2. Листья на деревьях всегда зеленые?
3. Машина всегда обгонит пешехода?

Использование открытых задач способствует формированию у воспитанников нестандартного мышление, позволяющего достигать метапредметных результатов.

Работа по группам.

Предлагаю вам разбиться на группы и выполнить задания. Раздать листы с заданиями.

Много зависит от правильной формулировки задачи. Противоречие в условии — главное требование открытой задачи. Остается добавить достаточность условия и корректность вопроса.

Задание 1. Поставьте вопрос к тексту или дополнить его, чтобы получилась открытая задача.

• Группа 1. На улицах нашего города растут березы, клены, тополя. Они не дают нам вкусных плодов. …(Зачем их сажать)
• Группа 2. «Поспели вишни в саду у дяди Вани…» И у дяди Вани сразу возникла проблема:…(как спасти урожай от скворцов)
• Группа 3. 50% суток я сплю, 2 часа я делаю макияж. Обед готовлю на 1 час дольше, чем занимаюсь уборкой, некоторое время любуюсь своей красотой… (Распределите время суток так, чтобы мне все успеть.)

Задание 2. В начале занятия мы сказали, что задачи в школьных учебниках — это, как правило, задачи закрытые. Рассмотрим несколько задач из учебника математики. Во власти учителя совершить с ними чудесное превращение. Предлагаю вам переформулировать условие задачи из школьного учебника, чтоб она стала открытой.

• Группа 1. Расстояние между двумя машинами, едущими по шоссе в противоположном направлении, 200 км. Первая машина двигается со скоростью 60 км/ч, вторая — 80 км/ч. Чему будет равно расстояние между ними через 1 час?
• Группа 2. Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 15°?
• Группа 3. Сумма двух чисел 96, а разность 18. Найдите эти числа.

В формулировке открытой задачи не должно быть готового утверждения, могут быть даны неполные или лишние данные, отсутствовать вопрос задачи, при её решении может возникнуть необходимость самостоятельно «добыть» числовые данные, исследовать ситуацию, обосновать, доказать утверждения, провести нестандартные рассуждения, обобщить задачу, придумать задачу, самостоятельно изобрести «новые» способы решения и т.д.

Задание 3. Открытые задачи универсальны. Они активизируют учеников, повышают интерес к изучаемому предмету. Их можно использоваться на любом из этапов урока (подготовки учащихся к активному и сознательному усвоению нового материала, усвоения новых знаний, закрепления нового материала, обобщения и контроля, рефлексии), а также на занятиях внеурочной деятельности. Предлагаю задачу, а вы должны определить в какой теме урока ее можно использовать.

• Группа 1. Какой год называется високосным? Определите, является ли 2084 год (или любой другой) високосным?
• Группа 2. Один рыбак купил себе новую удочку длиной 5 метров. Домой ему приходится добираться автобусом. Автобус очень большой, но в нем запрещено перевозить предметы длиной более 4-х метров. Удочка не разбирается и не гнется. Как можно упаковать удочку, чтобы провезти ее в автобусе?
• Группа 3. Хочу узнать массу одной горошины. Как я могу это сделать? У меня есть современные электронные весы, которые показывают вес даже очень легких предметов, но они не реагируют на одну горошину.

Решение и составление открытых задач позволяет ученикам выйти за пределы предмета «математика», овладеть общеучебными навыками, научиться решать практические задачи, связанные с различными жизненными ситуациями. Но нельзя построить весь процесс обучения только на открытых задачах. Нужно эффективно сочетать оба типа задач — открытые и закрытые.

Рефлексия

Составить синквейн

Закончить наше занятие хочется словами:

«Открытый мир — всегда задача,

Решай — и ждет тебя удача!»

Мастер-класс

«Просто. Сложно. Интересно»

(Слайд 1) Я начну свой мастер-класс со следующего эпиграфа: «Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным» (Блез Паскаль). Итак, мастер-класс называется «Просто. Сложно. Интересно.»

Практика моей работы показала, что чем интересней игровые действия, которые я использую на уроках, тем незаметнее и эффективнее закрепляются полученные знания.

Дети активны в восприятии задач-шуток, головоломок, логических упражнений, поэтому в своей работе для активизации детей я стараюсь использовать занимательный материал, ведь он не только развлекает детей, дает возможность отдохнуть, переключиться, но и заставляет их задуматься, развивает инициативу, стимулирует развитие нестандартного мышления, логику, воображение. Ведь без математики не может обойтись ни одна современная наука.

О, математика, земная,

Гордись, прекрасная, собой.

Ты всем наукам мать родная,

И дорожат они тобой.

Уважаемые коллеги, я приглашаю вас в удивительный мир математики, где и просто, и сложно, и очень интересно.

Попробуйте свои силы в математическом многоборье.

(Слайд 2)

1. Разминка (проводится для того, чтобы сохранить хорошее настроение, бодрость духа, математический настрой).

Предлагаю вам задачи, правильное решение которых чаще всего не требует никаких дополнительных знаний, – внимательно читайте условие задачи и попробуйте миновать расставленные ловушки.

(Слайд 3)

• Один господин писал о себе: «…пальцев у меня двадцать пять на одной руке, столько же на другой, да на ногах десять…»Почему он такой урод? (Ответ: Господин не поставил в одном месте двоеточие. В каком?)

(Слайд 4)

(Слайд 5)

• Два путешественника одновременно подошли к реке. У берега была привязана лодка, в которой мог переправиться только один человек. Путешественники не умели плавать, но каждому из них удалось переправиться через реку и пойти своей дорогой. Как могло это случиться? (Ответ: Они подошли к реке с разных сторон.)

(Слайд 6)

• Почему парикмахер в Женеве охотнее подстрижет двух французов, чем одного немца? (Ответ: Потому, что больше заработает.)

1. «Оригаметрия». (Слайд 7)

• Давайте посмотрим на обычный лист бумаги, как на средство обучения одному из сложных предметов – геометрии. Я хочу с вами поделиться, как искусство оригами помогает решать многие геометрические задачи. Сейчас мы с вами проведем небольшую работу:

Возьмите оранжевый треугольник, давайте попробуем сгибанием его построить биссектрису одного из углов. Постройте биссектрисы двух других углов. Разверните лист бумаги. Внимательно посмотрите на следы сгибов. Что вы можете сказать?

Все три сгиба прошли через одну точку.

Если вы все действия выполнили правильно, то биссектрисы пересеклись в одной точке.

Возьмите голубой треугольник. Проделаем аналогичную работу, только сгибать будем несколько иначе. В результате мы построили высоту. Повторите действия для двух других сторон. Разверните лист бумаги. Что вы можете сказать теперь?

Все три сгиба прошли через одну точку.

Если вы все действия выполнили правильно, то высоты также пересеклись в одной точке.

Возьмите зеленый треугольник. Для построения следующей линии нам нужно разделить сторону треугольника пополам, для этого совмещаем две вершины треугольника и делаем небольшой сгиб, отмечая тем самым середину стороны. Теперь сгибаем треугольник, так чтобы линия сгиба проходила через вершину треугольника и отмеченную точку. Как вы помните, такой отрезок называется медианой треугольника. Постройте еще две медианы треугольника. Вновь рассмотрим рисунок линий и убедимся, что медианы так же пересекаются в одной точке.

Еще раз посмотрели на все три треугольника, какой общий вывод можно сделать?

Итак, в течение одной минуты мы с вами научились строить основные линии в треугольнике, а также сформулировали теоремы о трех замечательных точках треугольника. Самое главное, выполняя эти практические задания, мы освоили простейшие приемы искусства оригами – складывания фигурок из бумаги.

(Слайд

• «Танграмм»:

Для следующего задания понадобятся и смекалка, и знание пословицы «Семь раз отмерь, один раз отрежь». Дается комплект, состоящий из семи фигур: три пары равнобедренных прямоугольных треугольников и один квадрат.

Задание. Из данных семи фигур составить квадрат и треугольник.

Ответ:

(Слайд 9)

1. Головоломки со спичками. (Слайд 10)

Коробка спичек – отличное пособие для геометрических развлечений, требующих находчивости и сообразительности. Из спичек можно составить всевозможные прямолинейные фигуры, превращать одну фигуру в другую путем перекладывания спичек.

(Слайд 11)

• На столе лежат 6 спичек. Расположите их так, чтобы в каждом горизонтальном ряду было: а) по 4, б) по 6. (Слайд 12)

(Слайд 13)

• Из шести спичек составьте 4 треугольника со сторонами, равными длине спички. (Ответ: Решение можно получить только с «выходом» в пространство.) (Слайд 14)

(Слайд 15)

• Фигура, изображенная на рисунке, составлена из 8 спичек, наложенных друг на друга. Снять две спички так, чтобы осталось 3 квадрата.

(Слайд 16)

• Исправьте равенство так, чтобы оно стало верным, не дотрагиваясь, ни до одной спички (нельзя поджигать, перемещать, передвигать и т.д.).

(Слайд 17)

• «Математическое исчезновение»:

На столе 3 треугольника. Уберите 2 спички, чтобы треугольников не стало.

(Ответ: Убираем 2 спички и делаем из них знак «равно». Один треугольник минус один треугольник, равняется ноль — треугольников не стало.) (Слайд 18)

(Слайд 19)

1. Все гениальное – просто!

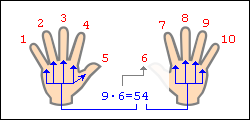
«Занимательная математика» может сделать интересными самые «скучные» вещи на свете, например, таблицу умножения.

Но умножение на 9 на пальцах – это нечто особенное. На фото выше продемонстрировано умножение 9 на 7. Загибаем 6 палец и сразу же видим ответ: первая цифра — количество пальцев слева от загнутого, вторая — справа. Итого 54!

(Слайд 20) Заключение:

В течение жизни мы решаем множество задач. И если каждую отдельно решенную задачу рассматривать, как распустившийся цветок, то в результате мы получим огромный, красивый букет.

Пусть все задачи, которые встают перед вами, будут решены, а букет будет только из распустившихся цветов.

Спасибо за плодотворную работу.

Мастер-класс для учителей

МОУ СОШ № 6 г. Магнитогорска на тему «Приемы мотивации учебной

деятельности

на уроках математики»

Астапова Светлана Викторовна, учитель математики

Как вы считаете, почему на один и тот же вопрос, люди, занимающиеся одной и той же работой, отвечали по — разному? Почему так вышло?

Случилось это в Средние века.

Монах, руководивший строительством собора, решил посмотреть, как работают каменщики.

Он подошел к первому и попросил его рассказать о своей работе.

— Я сижу перед каменной глыбой и работаю резцом. Скучная и нудная

работа, изнуряющая меня,- сказал тот со злобой.

Монах подошел ко второму каменщику и спросил его о том же.

— Я работаю по камню резцом и зарабатываю этим деньги. Теперь моя

семья не будет голодать,- ответил мастер сдержанно.

Монах увидел третьего каменщика и спросил о его работе.

— Со стороны, кажется, что я режу камень. Но на самом деле я строю Храм, который простоит тысячу лет. Я строю будущее, — улыбнувшись, ответил третий каменщик.

Приемы мотивации учебной деятельности

на уроках математики

Астапова С. В.

Древняя мудрость гласит:

можно привести коня к водопою,

но заставить его напиться нельзя

Необходима мотивация,

чтобы обучающийся захотел получить знания, которые мы с Вами готовы ему передать, либо создать условия, чтобы он сам взял.

В работе над повышением мотивации я учитываю, что:

В памяти ученика остаётся:

¼ часть услышанного материала

1/3 часть увиденного материала

½ часть услышанного и увиденного одновременно материала

¾ материала, если ко всему прочему ученик вовлечён в активные действия в процессе обучения

Применяю следующие приёмы повышения мотивации на уроке:

• устный счёт с включением задач, которые решаются с опорой на их жизненный опыт, на их смекалку ;
• игра на исправление преднамеренно сделанных ошибок в решении;
• упражнения на восстановление частично стертых записей, найди недостающий факт для достоверности;
• предлагаю задания и ответы к ним, среди которых есть

как верные, так и неверные.

• решаем игровые и занимательные задачи;
• решаем задания из открытого банка заданий ЕГЭ и ГИА;
• стремлюсь содержание задачи связать с реальными повседневными задачами;
• использую метод целенаправленной ошибки;

Применяю следующие приёмы повышения мотивации на уроке:

• привлечение учащихся к проектной деятельности;
• применяю исторические вставки( ребята готовят сообщения из истории развития математики, или факты по теме урока) ;
• привлекаю к участию в олимпиадах и конкурсах

различного уровня.

Одним из путей повышения интереса к предмету и
активности обучения является использовании эпиграфа

В качестве эпиграфов к уроку использую цитаты, изречения выдающихся людей.

Уважаемые коллеги, я предлагаю вашему вниманию несколько эпиграфов. Подумайте и попробуйте объяснить, как они могут работать на уроке.

• «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их!» (Д. Пойа)
• Дорогу осилит идущий, а математику — мыслящий.
• С малой удачи начинается большой успех.
• «Для того чтобы усовершенствовать ум, надо больше рассуждать, чем заучивать» ( Р.Декарт).
• Корень учения горек, зато плод его сладок.

Эпиграф, использованный в начале урока, становится мобилизатором внимания, настраивает на предстоящую работу, делая ее значимой, поскольку включает учеников в обсуждение. Этот прием насыщает материал урока, создает проблемные ситуации, заставляет думать и высказывать свои мысли. Эпиграф служит не только обучающей, но и развивающей, воспитательной целью урока.

АССОЦИАЦИИ
Введение математических терминов

«Точка» – лат. “пункт” – пунктир; “пунктум” – укол, медицинский термин “пункция” – прокол)

«Конус» — это латинская форма греческого слова «конос», означающего сосновую шишку

«Цилиндр» — латинская форма греческого слова «кюлиндрус», означающий «валик», «каток»

«Радиус» — «спица колеса»

МАТЕМАТИЧЕСКИЙ РЕБУС

Подсказка. МУРАВЕЙ ВЕНИК

Прием «Лови Ошибку»

По теме: «Сложение чисел с разными знаками»

Найдите ашибки:

• 0,3 + (-1,2) =0,9
• 1 + (-0,3) = 0,61
• 26 + (-6) = -20

Восстановите частично стертые записи:

+ (-1,2) =0,9

1 + ( ) = 0,61

26 + (-6) =

Прием «Кластер»

Уважаемые коллеги, я предлагаю вам составить по теме уравнения кластер (обобщить виды уравнений, способы решения)

Уравнения

Неполные

<number>

Уравнения ивда

а в

х  х  с, а,в  0

Продукт, полученный на уроке в 8 классе

Уравнения

Линейные

ах  в  0, а  0, х   в

а

Квадратные

• в  Д

2а

Д  в2  4ас, х 

ах2  вх  с  0, а  0

ах 2  с  0, х    с ,  с  0

а а

в а

Неполные

ах 2  вх  0, а  0, х  0 или х  

Уравнения вида

х  х  с, а,в  0

а в

Иррациональные уравнения: 1.Возвести в квадрат обе части уравнения

• Решить полученное рациональное
• Сделать проверку. Отсеять посторонние

Рациональные

вида =0

<number>

Софизм

<number>

• Одним из методических приемов, направленных на формирование мотивации школьников является приём создания и решения проблемных ситуаций. Для формирования мотивации интереса использую проблемные ситуации, представленные в виде софизмов, которые я предлагаю вашему вниманию.

Уважаемые коллеги, здесь представлены доказательства, в которых

допущены ошибки, в результате которых получен неверный ответ.

Найдите ошибки.

<number>

1. Пример: 4=5

Доказательство: имеем числовое тождество 4:4=5:5. Вынесем за скобки общий множитель 4(1:1 )=

5(1:1). Числа в скобках равны, их

Парадокс…

2. Докажем, что 5 = 4. Пусть х = 1/3, тогда 3х = 1.

Представим 3х как 15х – 12х, и

1 – как 5 – 4, тогда вместо равенства

3х = 1 можно записать 15х – 12х = 5 – 4.

можно сократить, получим: 4=5 (!?). Решим это уравнение:

15х – 5 = 12х – 4,

5(3х – 1) = 4(3х – 1).

Разделим обе части равенства на (3х – 1) и получим 5 = 4.

• Ошибка сделана при вынесении общих множителей 4 из левой части и 5 из правой части

<number>

• Поделили на выражение 3х – 1 , которое при х = 1/3 равно нулю

Данный софизм можно использовать при изучении темы

«Уравнение и его свойства».

Этот приём позволяет активизировать познавательную деятельность

учащихся, которые получают задание объяснить, в чём ошибка. Удивление стимулирует активную работу детей. Решая софизм, они совершенствуют умение сопоставлять, сравнивать, наконец, оспаривать другие точки зрения, доказывать свою правоту

<number>

РЕФЛЕКСИЯ

<number>

Упражнение «Ладошка»

Коллеги обведите ладошку.

Каждый палец – это какая-то позиция. На нужной позиции нарисовать колечко.

Большой – мне было не интересно

Указательный – я получила конкретные рекомендации по теме

Средний – мне было трудно включиться в работу Безымянный — для меня это было важно и интересно Мизинец –недостаточно раскрыта тема

<number>

Литература:

• Асеев, В.Г. Мотивация поведения и формирование личности Текст. / В.Г. Асеев. -М.: Мысль, 1976. 158 с
• Брадис, В.М. Методика преподавания математики в средней школе Текст. / В.М. Брадис. М.: Учпедгиз, 1954. — 504 с.
• Якиманская, И. С. Технология личностно-ориентированого образования Текст. / И. С. Якиманская. М.: Сентябрь, 2000. — 176с
• Якобсон, П. М. Психологические проблемы мотивации поведения человека Текст. / П. М. Якобсон. М.: Просвещение, 1969. — 317 с.

<number>

Мастер – класс учителя математики

Цель педагогической деятельности — повышение мотивации школьников посредством использования технологии развития критического мышления на уроках математики

Задачи:

• повышение интереса учащихся к процессу обучения и активного восприятия учебного материала;

• развитие мыслительных навыков учащихся, необходимых для учёбы и обычной жизни;

• разработка занятий по математике с использованием технологии развития критического мышления.

Мы с Вами рассмотрим применение следующих приёмов:

1. на стадии Вызов — игра «Верю – не верю»,

2. на стадии Осмысления — сочетание приёмов «Кластер» и «Решето» , «Чтение текста с пометками», игра «Верю – не верю»,

3. на стадии Рефлексии — «Шесть шляп мышления».

Ход мастер-класса

1.Доброе утро, Уважаемые коллеги. Хочу вас познакомить с теми приемами, которые использую на своих уроках. Попрошу вас представить учащимися класса на уроке геометрии. Тема урока «Квадрат».

2.Стадия Вызов, этап актуализации знаний.

Давайте мы с вами сыграем в игру «Верю — не верю». Будьте внимательны, если верите мне, то хлопайте в ладоши, если не верите, то топайте ногами.

Верите ли вы, что у квадрата все стороны равны?

Верите ли вы, что сумма углов квадрата равна 360^о?

Верите ли вы, что диагонали квадрата перпендикулярны?

Верите ли вы, что отрезок — это изображение квадрата?

Верите ли вы, что квадрат может летать?

Спасибо.

3.Следующая стадия – Осмысление.

( приём «Кластер».)

Сейчас мы поработаем в группах. Проведем практическую работу

( работа в группах-парах)

• У Вас на столах лежат конверты с заданиями, достаньте их содержимое. Вам необходимо выполнить задание и заполнять схему – таблицу Кластер.

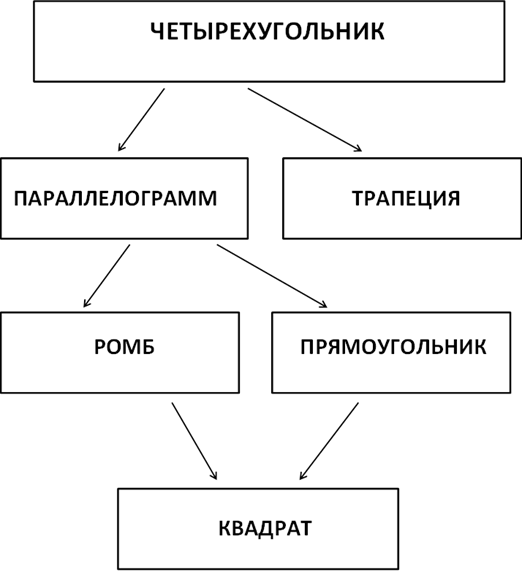
• (Разделите все четырехугольники на две группы. По какому принципу Вы это сделали? (параллелограммы и трапеции).

• Параллелограммы – ещё на две группы (прямоугольники и ромбы)

• Одна фигура может попасть и в одну группу, и в другую. Что это за фигура? (Квадрат).)

Итак Сформулируйте тему урока. (Квадрат)

В результате работы составляется кластер, например,

А теперь сравните вашу схему с верной -(слайд)

4.Приём «Чтение текста с пометками» (одновременно мы будем проводить физкультминутку). (Приложение 1) .

На столе у каждого есть листок с текстом. Вам нужно его прочитать. При этом – если информация вам не известна, поставив знак вопроса в тексте. (обсуждение вопросов, которые возникли в ходе чтения текста: Что вы уже знали ? 2. Что для вас было новым?

5.Для подведения итогов на стадии рефлексии мы воспользуемся приёмом «Шесть шляп мышления»

Я прошу вас одеть «шляпы» и высказать ваше мнение в соответствии с тем, как этого требует ваша шляпа.

(слайдБелая шляпа: ИНФОРМАЦИЯ

Что узнали? Чему научились?

Красная шляпа: ЭМОЦИИ, ЧУВСТВА, ИНТУИЦИЯ

Какие у меня по этому поводу возникают эмоции, чувства?

Желтая шляпа: ПОЗИТИВ

Что было хорошего и почему?.

Зеленая шляпа: КРЕАТИВНОСТЬ

Я сделал(а) бы это так…

Синяя шляпа: ПРОЦЕСС

Чего мы достигли?

Черная шляпа: КРИТИКА

Я не понял(а)…)

Учитель :Мы обучаем детей разным предметам: математика, русский язык, история и другие, но есть самая важный предмет, который они изучали, изучают и будут изучать. А мы, учителя, должны помочь им в достойном освоении этой дисциплины. И это – жизнь. С помощью технологии критического мышления я стараюсь научить детей думать, анализировать, предлагать, критиковать и воспринимать критику. Значит мы, Не для школы, для жизни учимся.

Спасибо за внимание.

Приложение 1

Текст «Квадрат»

Что такое квадрат?

В геометрии:

Квадрат – это прямоугольник, у которого все стороны равны.

В алгебре:

Квадратом числа а называется произведение двух множителей, каждое из которых равно а, т.е. а2=а .а

В других областях:

Дворовая игра с мячом; единица музыкального метра, равная 4,8, 16,32 тактам; разновидность джазовой импровизации

Какими свойствами обладает квадрат?

Все стороны квадрата равны, противоположные параллельны.

Все углы квадрата прямые.

Диагонали квадрата пересекаются и точкой пересечения делятся пополам.

Диагонали квадрата равны и взаимно перпендикулярны.

Диагонали квадрата делят углы пополам.

Дополнительные сведения о квадрате

У квадрата четыре угла по 900, значит, сумма углов квадрата равна 3600

9131- квадратный юбилей, так как

9131дней = 25 лет x 365 дней + 6 дней (високосный год)

В зависимости от того, в какой плоскости находится квадрат, он может быть изображен в виде отрезка.

С квадратом можно и поиграть. Шахматы, оригами, магические квадраты и многое другое.

А, сделав из него самолетик, он может и полетать.

Мастер-класс «Как провести мастер-класс по теме «Компетентностно-ориентированные задания на уроках математики, как фактор развития предметной грамотности учащихся»»